⚡DP란?
메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 상승시키는 방법입니다.
이미 계산 된 결과(작은 결과)를 별도의 메모리공간에 저장해두고
그 결과가 필요할때 꺼내서 사용하여 다시 계산하지 않도록 하며
일반적으로 탑다운 방식과 바텀업 방식 두가지 방식으로 구현됩니다.
⚡동적계획법이면 자료구조에서 말하는 동적 할당이랑 비슷한거임?
아니오
자료구조에서의 동적할당은 프로그램이 실행되는 도중 실행에 필요한 메모리를 할당하는 기법
을 말합니다.
하지만 동적계획법에서 동적(Dynamic)은 그냥 별 의미 없이 사용된 단어입니다.
⚡DP 이거 언제 쓸 수 있음?
1. 최적 부분 구조(Optimal Substructure)와
2. 중복되는 부분 문제(Overlapping Subpromblem) 두 조건이 만족될 때 사용할 수 있습니다.
* 최적 부분 구조?
큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있음
최적 부분 구조일때 그 문제의 답을 그 문제의 작은 문제의 답을 모으는걸로 해결할 수 있다는 뜻
그리디 알고리즘을 쓰려면 그때그때 최적해만을 모아도 최적의 답을 구할 수 있어야하잖슴?
그런걸 말하는듯
*중복되는 부분 문제
동일한 작은 문제를 반복적으로 해결해야 함
예컨대 피보나치 수열과 같은 문제를 해결하고자할때 우리는 값이 조금만 높아져도
피보나치수열의 f(1) , f(2)를 엄청나게 많이 구해야함
하지만 2번째 피보나치 수, 3번째 피보나치 수 등등을 기억해두고 불러와서 사용할 수 있다면
우리는 한번만 피보나치수를 구해도 될것임!!
⚡메모이제이션 쓴다는데 그게 뭐임?
메모이제이션 (Memoization) 은 다이나믹 프로그래밍을 구현하는 방법 중 하나로
한 번 계산한 결과를 메모리 공간에 메모하는 기법을 말합니다.
값을 기록해 둔다는 점에서 캐싱(cashing)이라고도 부릅니다.
⚡분할정복이랑 비슷해보이는데 분할정복이랑 뭔차이임?
* 둘의 공통점
DP와 분할정복은 최적 부분 구조를 가질 때 사용할 수 있다는 공통점이 있습니다.
큰 문제를 작은 문제로 나눌 수 있고 작은 문제의 답을 모으면 큰 문제를 해결할 수 있을 때 사용할 수 있죠!
*둘의 차이점
DP와 분할 정복의 차이점은 부분 문제가 중복되느냐 아니냐입니다.
DP에서는 각 부분 문제들이 서로 영향을 끼치며 부분 문제가 중복됩니다.
하지만 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않습니다.
⚡DP 문제 어케 푸는건데..
가장 먼저 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 풀 수 있는지 검토합니다.
만약 풀이 방법이 떠오르지 않는다면 다이나믹 프로그래밍을 고려합니다.
⚡예제 한번 보여줘요
프로그래머스의 멀리 뛰기 문제를 보겠습니다.
사실상 피보나치 수열 문제라고 봐도 무방한 문제에요

멀리뛰기라고 하지만 사실 문제를 잘 살펴보면 패턴을 알 수 있습니다.
1칸 혹은 2칸만 갈 수 있다고 가정하고 n을 1부터 차례차례 키워보면?
1일때는 1
2일때는 2
3일때는 3
4일때는 5
5일때는 8
엥..이거완전..? 피보나치수아니냐??
그럼 피보나치수를 dp로 구현하면 되겠네용
function solution(n) {
let dp = new Array(n+1).fill(null)
dp[1] = 1
dp[2] = 2
for(i=3 ; i<=n ; i++) {
dp[i] = (dp[i-2] + dp[i-1]) % 1234567
}
return dp[n]
}저는 인덱스랑 n이랑 일치하게 값을 쌓아올리고싶어서
일부러 dp[0]은 비워두고 문제를 풀었습니다.
dp를 모를땐 이게뭐농이었지만 간단한 풀이입니다.
dp[i]인덱스에 각각 대응되는 피보나치값들을 넣어두고
i가 증가해서 다음 인덱스로 넘어갈땐 단순히 i-2 , i-1의 값들을 더해주기만하면 되는 구조에요
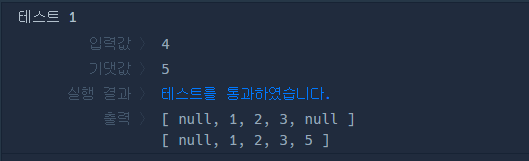
테케로 보면 더 쉽습니다.
i가 3일때 dp[3]의 값은 dp[1] + dp[2]입니다.
dp[1]은 값이 1 dp[2]는 값이 2니까
dp[3]은 3이되고 이 과정을 n까지 쭉 반복하는거죠!
반응형
'자료구조와 알고리즘' 카테고리의 다른 글
| 탐욕 알고리즘 (Greedy Algorithm) (0) | 2022.12.13 |
|---|
